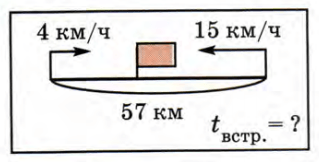
Из пункта A в пункт B отправился пешеход со скоростью 4 км/ч. Одновременно c ним из пункта B в пункт A отправился велосипедист со скоростью 15 км/ч. Через сколько часов встретились пешеход и велосипедист, если расстояние между пунктами 57 км?
Решение:
1) 4 + 15 = 19 (км/ч) − скорость сближения;
2) 57 : 19 = 3 (ч) − прошло до встречи.
Ответ: через 3 часа
 
Обратная задача 1.
Из пункта A в пункт B отправился пешеход со скоростью 4 км/ч. Одновременно c ним из пункта B в пункт A отправился велосипедист и встретился с пешеходом через 3 часа. Найдите скорость велосипедиста, если расстояние между пунктами 57 км?
Решение:
1) 57 : 3 = 19 (км/ч) − скорость сближения;
2) 19 − 4 = 15 (км/ч) − скорость велосипедиста.
Ответ: 15 км/ч
 
Обратная задача 2.
Из пункта A в пункт B отправился пешеход. Одновременно c ним из пункта B в пункт A отправился велосипедист со скоростью 15 км/ч и встретился с пешеходом через 3 часа. Найдите скорость пешехода, если расстояние между пунктами 57 км?
Решение:
1) 57 : 3 = 19 (км/ч) − скорость сближения;
2) 19 − 15 = 4 (км/ч) − скорость пешехода.
Ответ: 4 км/ч
 
Обратная задача 3.
Из пункта A в пункт B отправился пешеход со скоростью 4 км/ч. Одновременно c ним из пункта B в пункт A отправился велосипедист со скоростью 15 км/ч. Найдите расстояние между пунктами, если пешеход и велосипедист встретились через 3 часа?
Решение:
1) 4 + 15 = 19 (км/ч) − скорость сближения;
2) 19 * 3 = 57 (км) − расстояние между пунктами.
Ответ: 57 км
 
Существует 3 обратные задачи.