
ЗАДАЧА−ИССЛЕДОВАНИЕ
Число диагоналей многоугольника можно подсчитать так:
• найти число диагоналей, выходящих из одной вершины, − их на 3 меньше, чем вершин (рисунок справа);
• умножить это число на число вершин;
• разделить результат на 2 (объясните почему).
Сколько диагоналей у семиугольника? десятиугольника? стоугольника? У какого многоугольника 9 диагоналей?
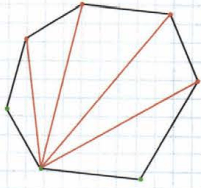

При подсчете каждая диагональ учитывается 2 раза, так как диагональ соединяет 2 вершины многоугольника и подсчет выполняется для каждой вершины. Поэтому полученный результат нужно разделить на 2.
Семиугольник:
1) 7 − 3 = 4 (диагонали) − выходит из каждой вершины;
2) 4 * 7 = 28 (диагоналей) − удвоенное количество;
3) 28 : 2 = 14 (диагоналей) − в семиугольнике.
Десятиугольник:
1) 10 − 3 = 7 (диагоналей) − выходит из каждой вершины;
2) 7 * 10 = 70 (диагоналей) − удвоенное количество;
3) 70 : 2 = 35 (диагоналей) − в десятиугольнике.
Стоугольник:
1) 100 − 3 = 97 (диагоналей) − выходит из каждой вершины;
2) 97 * 100 = 9700 (диагоналей) − удвоенное количество;
3) 9700 : 2 = 4850 (диагоналей) − в стоугольнике.
Пусть a (вершин) в многоугольнике, тогда:
1) a − 3 (диагоналей) − выходит из каждой вершины;
2) a(a − 3) (диагоналей) − удвоенное количество;
3) a(a − 3) : 2 = 9 (диагоналей) − в многоугольнике;
a(a − 3) = 9 * 2
a(a − 3) = 18
18 = 3 * 6 = 9 * 2
Путем подбора можно вычислить, что a = 6, т.к.:
6 * (6 − 3) = 18
6 * 3 = 18
Значит у шестиугольника 9 диагоналей.
Ответ: 14 диагоналей; 35 диагоналей; 4850 диагоналей; у шестиугольника.