
Представьте число 30 в виде суммы нескольких квадратных чисел. Сделайте рисунок.
■ Великий древнегреческий ученый Диофант (III в. н.э.) нашел закономерность, связывающую треугольные числа с квадратными числами: если треугольное число умножить на 8 и к произведению прибавить 1, то получится квадратное число. Коротко это можно записать так:
треугольное число * 8 + 1 = квадратное число.
Проверьте эту закономерность для нескольких первых квадратных чисел. Вы видели, что треугольные числа получаются суммированием последовательных натуральных чисел. А квадратные числа получаются суммированием последовательных нечетных чисел. В самом деле,
1 + 3 = 4,
1 + 3 + 5 = 9,
1 + 3 + 5 + 7 = 16,
1 + 3 + 5 + 7 + 9 = 25 и т.д.


1 + 4 + 9 + 16 = 30
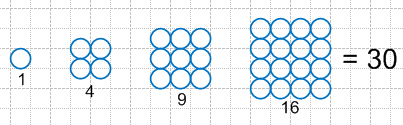
■
1 * 8 + 1 = 8 + 1 = 9
3 * 8 + 1 = 24 + 1 = 25
6 * 8 + 1 = 48 + 1 = 49
10 * 8 + 1 = 80 + 1 = 81