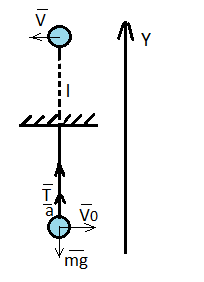
Изобразим все силы, действующие на шар: сила тяжести $\overrightarrow{mg}$, сила натяжения нити $\overrightarrow{T}$.
Запишем второй закон Ньютона в векторной форме:
$\overrightarrow{ma}=\overrightarrow{mg}+\overrightarrow{T}$;
Выберем ось Y перпендикулярно горизонтальной плоскости. Спроецируем уравнение на координатные оси:
T − mg = ma;
$a_{ц}=\frac{v_0^2}{l}$;
$T=ma+mg=\frac{m{v}_0^2}{l}+mg$;
По закону сохранения механической энергии:
$E_{к0}=E_{п}+E_{к}$;
$E_{к0}=\frac{m{v}_0^2}{2}$;
$E_{к}=\frac{m{v}^2}{2}$;
$E_{п}=mg\ast <!--\; \ast \; -->2l$;
$\frac{m{v}_0^2}{2}=mg\ast <!--\; \ast \; -->2l+\frac{m{v}^2}{2}$;
Шар движется по дуге окружности. В вехней точке:
$a=\frac{v^2}{l}=g$;
В этой точке на шар действует только сила тяжести. Поэтому:
$v^2=gl$;
$\frac{m{v}_0^2}{2}=2mgl+\frac{mgl}{2}=\frac{5mgl}{2}$;
$v_0^2=\frac{\frac{5mgl}{2}}{\frac{m}{2}}=5gl$;
$T=\frac{5glm}{l}+mg=6mg=6P$;
Вывод: «подвешенный на нити к центру вертикального круга шар не может вращаться по этому кругу, если нить не в состоянии выдержать силу натяжения, превышающую вес шара в 6 раз» (T = 6P).