
(Для работы в парах.) Проиллюстрируйте с помощью кругов Эйлера соотношение между множествами A и B и найдите пересечение и объединение этих множеств, если:
а) A − множество целых чисел, кратных 3, B − множество целых чисел, кратных 5;
б) A − множество целых чисел, кратных 3, B − множество целых чисел, кратных 15.
1) Распределите, кто выполняет задания для случая а), а кто − для случая б), и выполните их.
2) Проверьте друг у друга, верно ли выполнен рисунок и правильно ли найдены пересечение и объединение множеств A и B.
3) Исправьте ошибки, если они допущены.

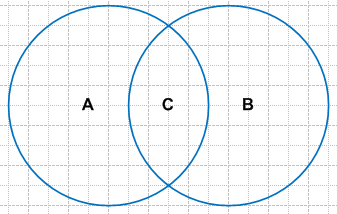
Множество чисел кратных 3: A = {n|n = 3k, k ∈ Z}.
Множество чисел кратных 5: B = {m|m = 5k, k ∈ Z}.
В пересечении будет множество чисел, кратных 15:
С = A∩B = {p|p = 15k, k ∈ Z}
В объединении будет множество чисел, кратных 3 и кратных 5:
AUB = {m,n|n = 3k, m = 5k, k ∈ Z}
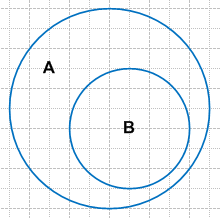
Множество чисел кратных 3: A = {n|n = 3k, k ∈ Z}.
Множество чисел кратных 15: B = {m|m = 15k, k ∈ Z}.
Множество B является подмножеством A: B⊂A.
Пересечением будет множество B: A∩B.
Объединением будет множество A: AUB = A.