
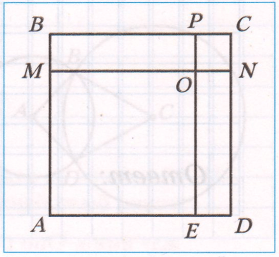
На рисунке четырехугольники ABCD и OPCN − квадраты, а четырехугольники MBPO и EOND − прямоугольники, AB = 10 см, CP = 2 см. Сколько процентов площади квадрата ABCD составляет площадь:
1) квадрата OPCN;
2) квадрата AMOE;
3) прямоугольника MBPO;
4) прямоугольника AMND?

1) 2 * 2 = 4 $(см^2)$ − площадь квадрата OPCN;
2) 10 * 10 = 100 $(см^2)$ − площадь квадрата ABCD;
3) $\frac{4}{100} * 100 = 4$ (%) − площади квадрата ABCD составляет площадь квадрата OPCN.
Ответ: 4%
Так как, ABCD и OPCN − квадраты, то:
AB = BC = CD = AD = 10 (см);
OP = PC = CN = ON = 2 (см);
MO = BC − PC = 10 − 2 = 8 (см), тогда:
1) 8 * 8 = 64 $(см^2)$ − площадь квадрата AMOE;
2) 10 * 10 = 100 $(см^2)$ − площадь квадрата ABCD;
3) $\frac{64}{100} * 100 = 64$ (%) − площади квадрата ABCD составляет площадь квадрата AMOE.
Ответ: 64%
Так как, ABCD и OPCN − квадраты, то:
AB = BC = CD = AD = 10 (см);
OP = PC = CN = ON = 2 (см);
BP = BC − PC = 10 − 2 = 8 (см), тогда:
1) 8 * 2 = 16 $(см^2)$ − площадь прямоугольника MBPO;
2) 10 * 10 = 100 $(см^2)$ − площадь квадрата ABCD;
3) $\frac{16}{100} * 100 = 16$ (%) − площади квадрата ABCD составляет площадь прямоугольника MBPO.
Ответ: 16%
Так как, ABCD и OPCN − квадраты, то:
AB = BC = CD = AD = 10 (см);
OP = PC = CN = ON = 2 (см);
ND = CD − CN = 10 − 2 = 8 (см), тогда:
1) 8 * 10 = 80 $(см^2)$ − прямоугольника AMND;
2) 10 * 10 = 100 $(см^2)$ − площадь квадрата ABCD;
3) $\frac{80}{100} * 100 = 80$ (%) − площади квадрата ABCD составляет площадь прямоугольника AMND.
Ответ: 80%