
Докажите, что сумма длин двух противоположных сторон выпуклого четырехугольника меньше суммы длин его диагоналей.

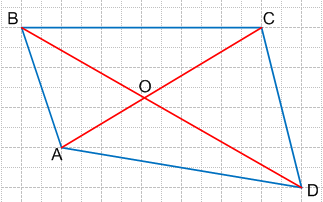
Дано:
ABCD − выпуклый четырехугольник.
Доказать:
AB + CD < AC + BD
Доказательство:
Точка O − точка пересечения диагоналей.
Из неравенства треугольника можем записать:
AB < AO + BO;
CD < OC + OD.
Найдем сумму этих двух неравенств:
AB + CD < AO + BO + OC + OD = (AO + OC) + (BO + OD) = AC + BD
То есть:
AB + CD < AC + BD
Неравенство доказано.